如何通过统计分析洞察超市消费者行为：以宽广超市为例

在超市运营中，理解消费者的购物行为是制定营销和运营策略的关键。本文以宽广超市为例，通过一组示例数据，使用平均数、中位数、四分位数、众数和标准差等统计方法，教你如何分析消费者消费金额，挖掘关键洞察。

一、示例数据

假设宽广超市收集了20位顾客的单次消费金额（单位：人民币，元）：

1

20, 25, 30, 30, 35, 40, 45, 50, 50, 50, 55, 60, 65, 70, 80, 90, 100, 120, 150, 200

这组数据模拟了超市消费的正偏态分布：大部分为小额日常消费（如食品、日用品），少数为高额消费（如批量采购）。

二、统计分析方法与结果

1. 平均数：总体消费水平

计算：平均数 = 数据总和 ÷ 样本数
总和 = 1,205元，样本数 = 20，平均数 = 1,205 ÷ 20 = 60.25元。

洞察：平均客单价约60.25元，反映总体消费水平，但受高额消费（如200元）影响，可能高估典型消费者的购物金额。

2. 中位数：典型消费水平

计算：将数据排序后取中间值（第10和第11个数据：50和55），中位数 = (50 + 55) ÷ 2 = 52.5元。

洞察：中位数52.5元比平均数低，更准确反映普通消费者的消费水平，适合正偏态分布的数据。超市可围绕50元设计促销。

3. 四分位数：消费分布与客户分层

计算：

  • Q1（25%）：第5和第6个数据（35和40），Q1 = 37.5元。
  • Q2（50%）：即中位数，52.5元。
  • Q3（75%）：第15和第16个数据（80和90），Q3 = 85元。
  • 四分位距（IQR）：Q3 - Q1 = 85 - 37.5 = 47.5元。
  • 异常值：大于Q3 + 1.5IQR = 85 + 1.547.5 = 156.25元的数据（150元、200元）。

洞察：

  • 中间50%消费者的消费金额在37.5元到85元，超市可针对此区间优化商品和促销。
  • 异常值（150元、200元）可能是团购或高价值客户，需单独分析。
  • IQR=47.5元表明消费分布较宽，消费者行为有一定差异。

可视化：使用箱线图展示Q1、Q2、Q3和异常值，直观反映分布和离散程度。以下是生成箱线图的Python代码：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16

import matplotlib.pyplot as plt

# 设置中文字体，支持中文显示
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False

# 示例数据
data = [20, 25, 30, 30, 35, 40, 45, 50, 50, 50, 55, 60, 65, 70, 80, 90, 100, 120, 150, 200]

# 绘制箱线图
plt.boxplot(data, vert=True, patch_artist=True)
plt.title("宽广超市消费金额箱线图")
plt.ylabel("消费金额（人民币）")
plt.grid(True, linestyle='--', alpha=0.7)
plt.savefig("boxplot.png")  # 保存图像
plt.show()

运行上述代码后，生成的箱线图如下：

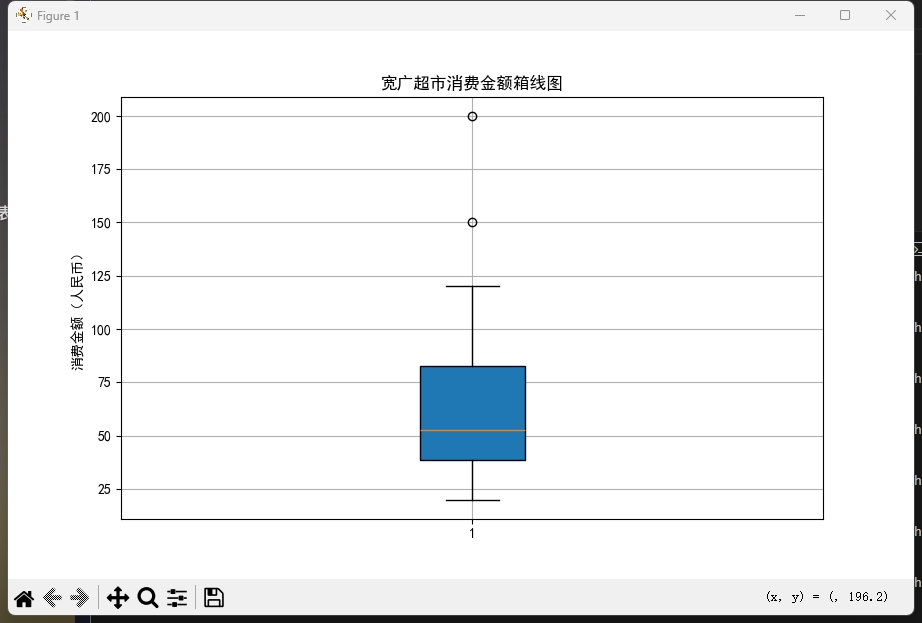
宽广超市消费金额箱线图

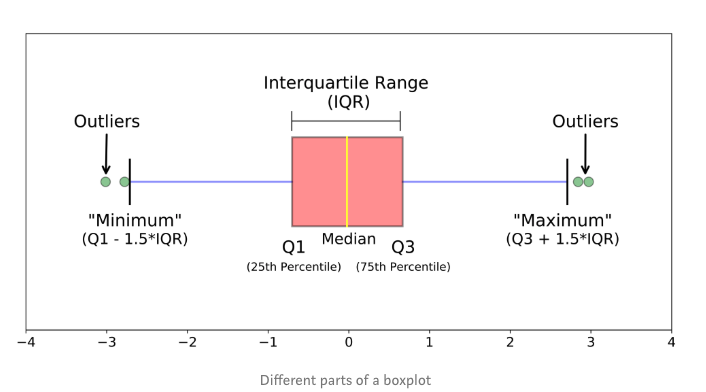
箱线图说明：

  • 底部横线（下须线末端）：最低非异常值（约20元）。
  • 箱体底部（Q1）：第一四分位数（37.5元）。
  • 箱体中线（Q2）：第二四分位数（中位数，52.5元）。
  • 箱体顶部（Q3）：第三四分位数（85元）。
  • 顶部横线（上须线末端）：最高非异常值（约120元）。
  • 异常值点：150元和200元（超出Q3 + 1.5*IQR = 156.25元）。

4. 众数：最常见消费金额

计算：50元出现3次，众数 = 50元。

洞察：50元是最常见的消费金额，表明许多消费者倾向于中等金额购物（如购买食品、日用品）。超市可推出50元左右的优惠套餐,刺激复购。

5. 标准差：消费波动程度

计算：标准差 = √(偏差平方和 ÷ 样本数)
偏差平方和 = 37,227.5，方差 = 37,227.5 ÷ 20 = 1,861.375，标准差 ≈ 43.14元。

洞察：标准差43.14元较高，说明消费金额波动大，存在小额消费（20元）和大额消费（200元）的差异，消费者行为异质性高。

可视化：直方图显示正偏态分布，结合众数观察消费集中点（可通过额外代码生成，略）。

三、综合洞察与策略建议

通过以上分析，宽广超市可以得出以下洞察：

  • 平均数（60.25元）：适合评估整体收入，但不代表典型消费。
  • 中位数（52.5元）和众数（50元）：提示普通消费者集中在50元左右，超市可推出“满65赠X”促销。
  • 四分位数（Q1=37.5, Q3=85）：
    • 中间50%消费在37.5-85元，适合设计组合套餐。
    • 异常值（150元、200元）提示高价值客户，可提供会员折扣。
  • 标准差（43.14元）：消费波动大，需细分客户：
    • 小额消费者（<37.5元）：推广低价日用品。
    • 高额消费者（>85元）：提供精细化服务或满赠。

策略建议：

  1. 促销设计：推出“满65减X”或“39元套餐”，覆盖中位数和众数消费者。
  2. 客户分层：
    • 低价值客户（<37.5元）：推广低价商品。
    • 高价值客户（>85元）：提供积分或专属折扣。
  3. 库存管理：高标准差提示需求波动，动态调整生鲜等热门商品库存。
  4. 异常值分析：针对150元以上的大额消费，分析是否为团购或特定商品（如家电），制定针对性营销。

四、总结

通过平均数、中位数、四分位数、众数和标准差，超市可以全面了解消费者行为的分布、集中点和异质性，但绝不是平均客单价那么简单。这些统计方法依然简单易用，却能为定价、促销和库存管理提供有力支持。希望我的这篇文章能帮助你掌握数据分析的实用技巧，优化超市运营！

如果你有更多数据或想深入分析某一方面，欢迎留言讨论！